Logarithms and Exponential Functions Quiz: 10 Questions to Test Your Math Skills
Logarithms, natural logarithms (ln), and exponential functions serve as the backbone of modern mathematics, physics, computing, finance, and data science. A logarithms quiz like this one helps learners test their understanding of concepts that appear in everything from computer algorithms to radioactive decay, population growth, signal processing, and compound interest. These functions are not just abstract ideas— they are practical tools that describe how real-world systems behave.

Logs and exponentials are inverses of each other, meaning one undoes the action of the other. If exponential functions describe fast growth or decay, logarithms describe slow, compressive behavior that allows us to manage extremely large numbers.
What Are Logarithms?
A logarithm answers the question: “To what power must we raise the base to obtain a given number?”
For example, log10(100) = 2 because 10² = 100. This powerful concept allows us to express huge or tiny values in a manageable way. Logarithms help scientists simplify calculations of pH in chemistry, the Richter scale in geology, and even decibel levels in sound engineering.
For a deeper breakdown, see Britannica’s detailed explanation of logarithms:
https://www.britannica.com/science/logarithm
Natural Logarithms and the Number e
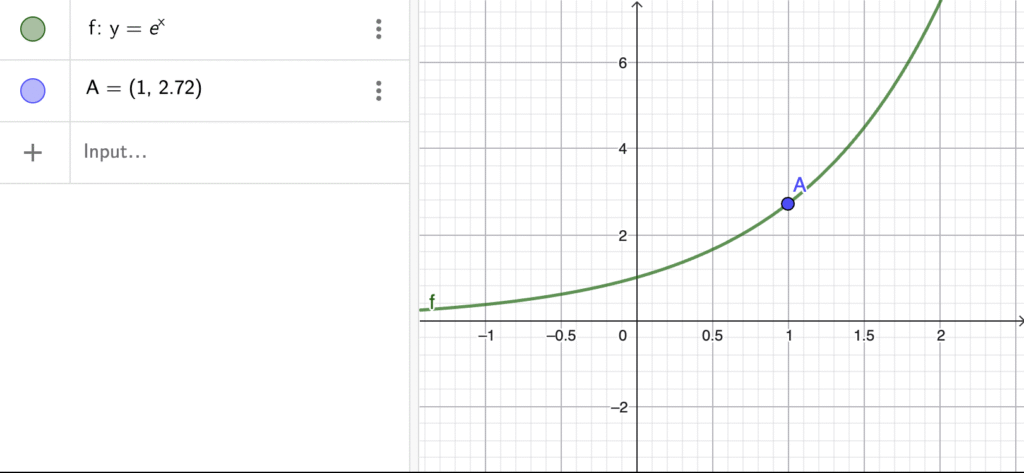
The natural logarithm, written ln(x), is the logarithm with base e, where e is approximately 2.718281828. The number e is fundamental because it arises naturally in growth processes: population models, radioactive decay, interest formulas, and even how heat diffuses.
The natural log represents the time it takes for exponential processes to reach certain points. Its inverse function, e^x, models growth that accelerates proportionally to its current size—truly “growth feeding on itself.”
A complete explanation of the number e and natural logs can be found at:
https://mathinsight.org/e_exponential_growth
Exponential Functions: The Mathematics of Growth and Decay
Exponential functions are written as a^x or e^x. These functions describe systems where change is proportional to current size, such as bacteria doubling, money earning compound interest, or heat dissipating. Exponential growth accelerates rapidly, eventually outpacing polynomials like x² or x³.
Understanding exponential growth is essential in biology, finance, data science, and epidemiology. It helps explain why certain processes speed up dramatically after a slow beginning.
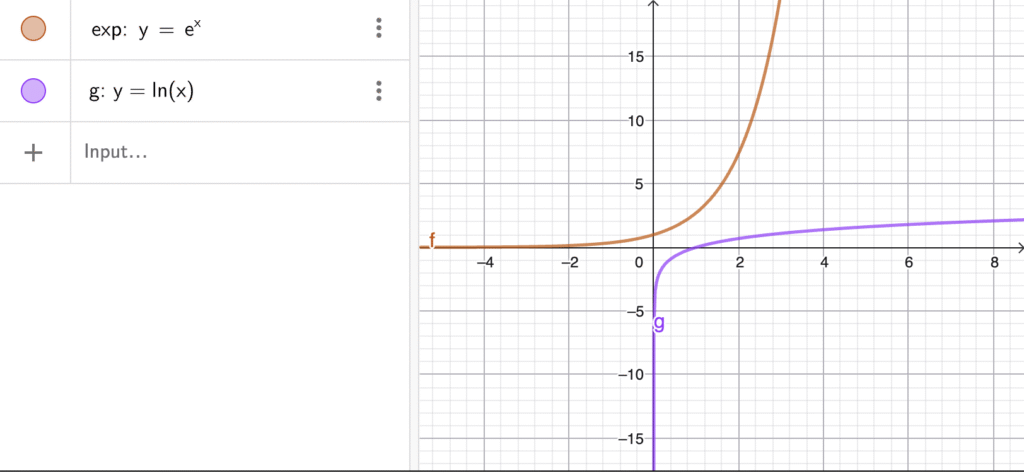
Logarithms as the Inverse of Exponentials
One of the quiz questions asks about the inverse of e^x, and the correct answer is ln(x). This inverse relationship is crucial because it allows us to solve equations where exponentials appear. If you have e^x = 20, you can find x by computing ln(20).
This inverse relationship is visually represented by symmetry across the line y = x—two curves reflecting each other.
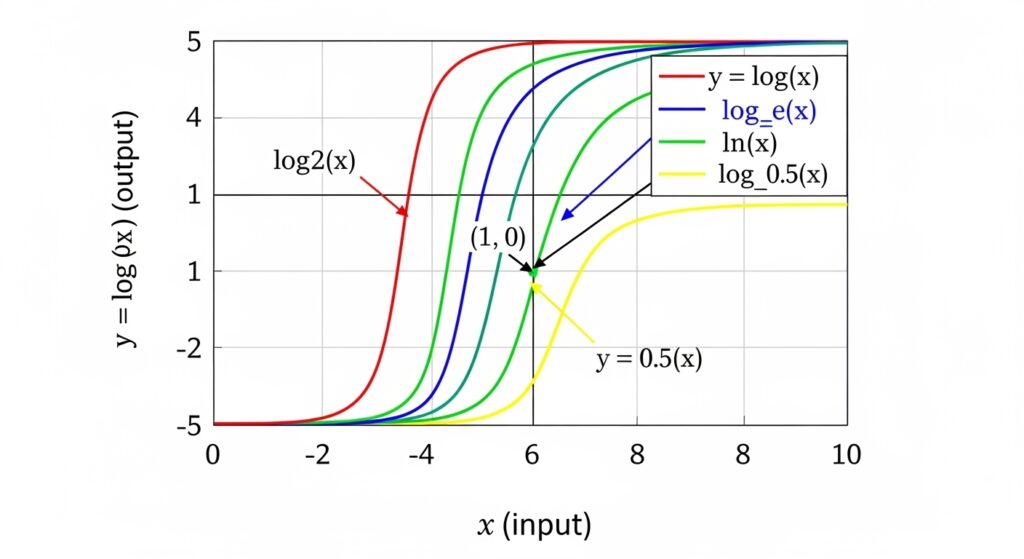
Common Logarithms, Natural Logs, and Binary Logs
Not all logs use the same base. Here are three main types:
- log10(x) — common logarithm (used in science and engineering)
- ln(x) — natural logarithm (base e, used in calculus and growth models)
- log2(x) — binary logarithm (used in computing and algorithms)
The quiz includes log2(8) = 3 because 2³ = 8. Binary logs appear constantly in complexity theory, such as O(log n) algorithms in computer science.
[image prompt: binary representation lines turning into logarithmic curves]
Key Logarithmic Identities and Properties
One of the fundamental laws of logarithms is:
log(a × b) = log(a) + log(b)This identity turns multiplication into addition, simplifying complex calculations. Before calculators, scientists relied on this rule to compute huge values by hand. Even today, logarithmic identities are essential for solving differential equations and optimization problems.
A useful list of log properties appears here:
https://www.khanacademy.org/math/algebra/x2f8bb11595b61c86:logs
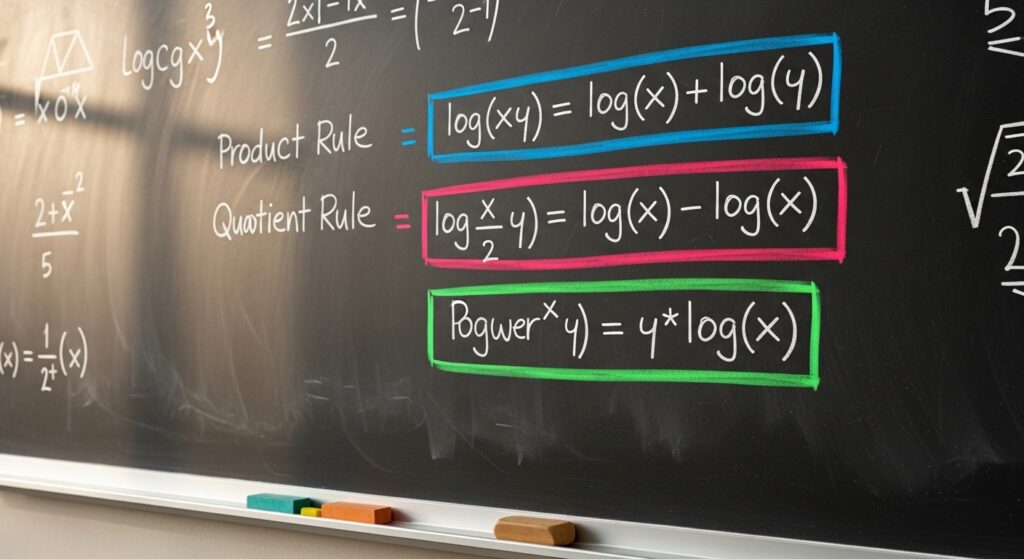
The Meaning of ln(1) and ln(e)
Two fundamental natural log values are featured in this quiz:
- ln(1) = 0 (because e⁰ = 1)
- ln(e) = 1 (because e¹ = e)
These values provide anchors for understanding the ln function. They show that natural logs translate exponential behaviors into linear relationships—a powerful tool in calculus.
[image prompt: ln graph crossing points (1,0) and (e,1)]
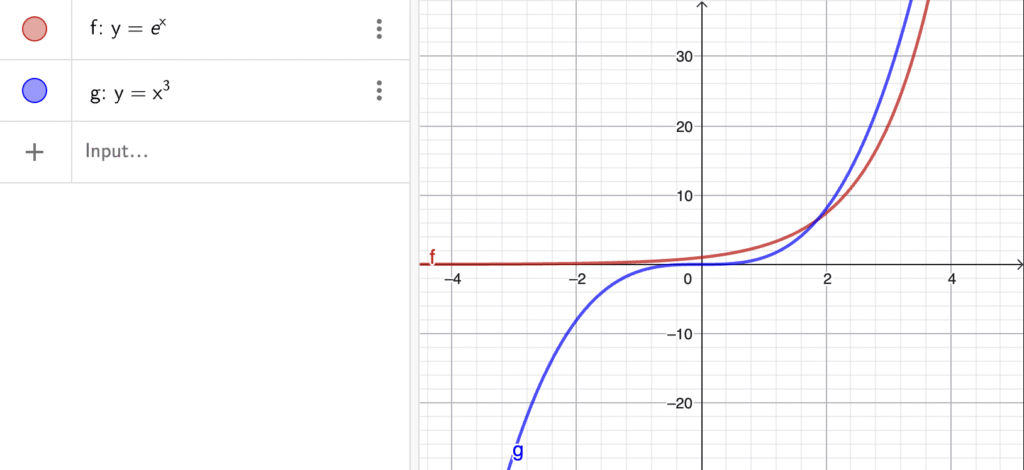
Why Exponential Functions Grow Faster Than Polynomials
A final quiz question compares e^x with x³. For small x, a polynomial may appear larger, but exponential functions eventually dominate because their rate of change increases proportionally to their value. This concept is critical in understanding computational complexity, viral growth, nuclear reactions, and investment compounding.
A helpful explanation of exponential dominance:
https://mathinsight.org/exponential_dominance_polynomial
Conclusion: Mastering Logs and Exponentials
Logarithms and exponential functions form one of the most important foundations of higher mathematics. They appear naturally in science, finance, biology, physics, programming, and engineering. By testing your understanding with this logarithms quiz, you strengthen your ability to analyze equations, interpret graphs, solve growth-and-decay models, and think critically about mathematical relationships. Whether you’re a student, a self-learner, or a math enthusiast, mastering logs and exponentials opens the door to deeper mathematical insight.







